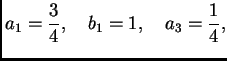Ako je ![]() neparna funkcija, onda je
neparna funkcija, onda je
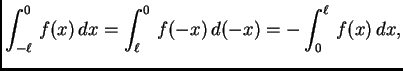
![$\displaystyle a_0 = \frac{1}{\ell}\,\int_{-\ell}^{\ell}\,f(x)\,dx = \frac{1}{\ell}\,\left[\int_{-\ell}^0\,
f(x)\,dx + \int_0^{\ell}\,f(x)\,dx\right] = 0.$](img1598.png)
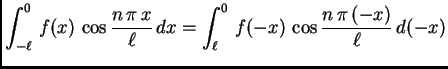
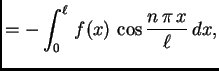
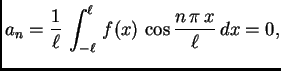 za
za 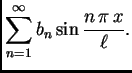
Osim toga
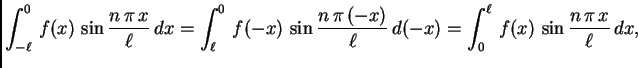
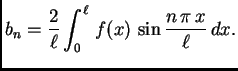
Slično bismo u slučaju parnosti funkcije dobili ![]() pa je
Fourierov red takve funkcije oblika
pa je
Fourierov red takve funkcije oblika
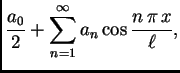
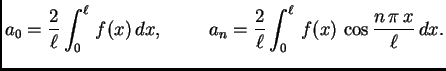
Rješenje. Tu se radi o proširenju po parnosti prvog brijega sinusne
funkcije. Period je ![]() pa su Fourierovi koeficijenti
pa su Fourierovi koeficijenti
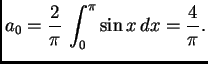
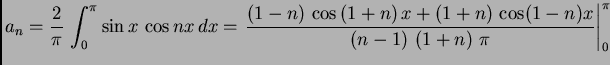
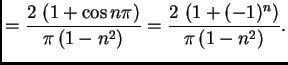
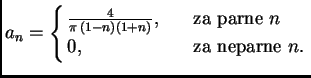
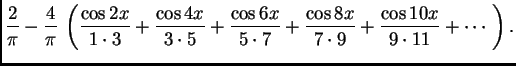
Rješenje. Svaki sumand od ![]() je potencija ili produkt potencija
trigonometrijskih funkcija perioda
je potencija ili produkt potencija
trigonometrijskih funkcija perioda ![]() što
je upravo duljina segmenta na kojem želimo napisati Fourierov red. U
tom slučaju je dovoljno svaki od sumanada napisati pomoću linearne
kombinacije trigonometrijskih funkcija višestrukog argumenta.
što
je upravo duljina segmenta na kojem želimo napisati Fourierov red. U
tom slučaju je dovoljno svaki od sumanada napisati pomoću linearne
kombinacije trigonometrijskih funkcija višestrukog argumenta.
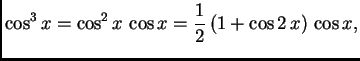
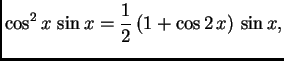
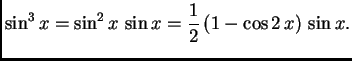
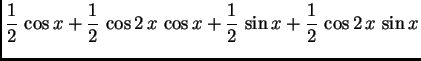 |
|||
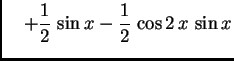 |
|||
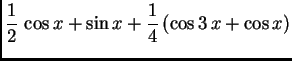 |
|||
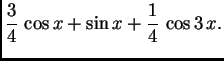 |