Next: Integracija supstitucijom
Up: Dodaci
Previous: Monotonost i derivacija
Contents
Index
Deriviranje integrala po gornjoj granici
Neka je
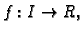 gdje je
gdje je 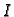 interval u
interval u 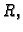 integrabilna
funkcija na
integrabilna
funkcija na ![$ [a,b].$](img3885.gif) Neka je
Neka je 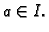 Za bilo koji
Za bilo koji 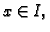 integral
funkcije
integral
funkcije  od
od 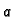 do
do  je broj koji ovisi o
je broj koji ovisi o 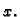 Tako imamo
funkciju
Tako imamo
funkciju
Funkcija 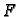 je primitivna funkcija od
je primitivna funkcija od 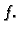 Doista,
U predzadnjoj jednakosti smo upotrebili integralni teorem srednje
vrijednosti.
Doista,
U predzadnjoj jednakosti smo upotrebili integralni teorem srednje
vrijednosti.
Prema tome funkcija 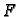 ima derivaciju, i vrijedi
ima derivaciju, i vrijedi
pa možemo zaključiti da derivacija integrala neprekidne funkcije po
gornjoj granici postoji i da je jednaka vrijednosti podintegralne
funkcije u gornjoj granici.
Da je bilo
onda bismo imali
pa bi bilo
Možemo zaključiti da je derivacija integrala neprekidne funkcije po
donjoj granici jednaka negativnoj vrijednosti podintegralne funkcije u
donjoj granici.
Salih Suljagic
2000-03-11
![]() gdje je
gdje je ![]() interval u
interval u ![]() integrabilna
funkcija na
integrabilna
funkcija na ![]() Neka je
Neka je ![]() Za bilo koji
Za bilo koji ![]() integral
funkcije
integral
funkcije ![]() od
od ![]() do
do ![]() je broj koji ovisi o
je broj koji ovisi o ![]() Tako imamo
funkciju
Tako imamo
funkciju
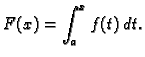
![$\displaystyle \lim_{\Delta{}x\rightarrow{}0} \frac{F(x+\Delta{}x)-F(x)}{\Delta{...
...} \frac{1}{\Delta x}\left[\int_a^{x+\Delta x}
f(t)\,dt-\int_a^x f(t)\,dt\right]$](img3888.gif)
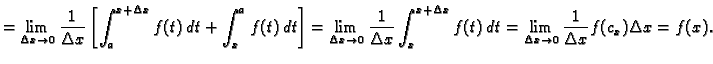
![]() ima derivaciju, i vrijedi
ima derivaciju, i vrijedi