Opis konstrukcije je za proračun stabilnosti gotovo jednak kao za statički proračun. Postoji, međutim, jedno važno ograničenje: zbog pretpostavki uvedenih pri definiranju geometrijske matrice krutosti elementa uzdužna sila mora biti na elementu konstantna, što znači da se koncentrirane sile u smjeru uzdužne osi elementa mogu zadati samo u njegovim čvorovima. (Naravno, raspodijeljeno opterećenje u smjeru osi ne može se zadati.)
Proračun stabilnosti provodi se izborom Buckling analysis
u izborniku Analysis. Program ispisuje aproksimaciju
najniže svojstvene vrijednost, lambda critical
(
![]() ), tako da je
aparoksimacija kritičnoga opterećenja
), tako da je
aparoksimacija kritičnoga opterećenja
Približni oblik izvijene konstrukcije (po dijelovima aproksimiran polinomima trećega stupnja) prikazuje se izborom Buckling mode u podizborniku Diagrams izbornika Analysis. Mjerila duljina i progiba mogu se mijenjati izborom Lenghts i Displacements u podizborniku Scale.
Kritična je sila za konzolu, kao što znamo,
Neka su: duljina
![]() = 5, 0 m, poprečni presjek
b/h = 10/10 [cm] i modul elastičnosti
E = 2 . 108 kN/m2; tada je
= 5, 0 m, poprečni presjek
b/h = 10/10 [cm] i modul elastičnosti
E = 2 . 108 kN/m2; tada je
![]() = 164, 493.
= 164, 493.

Modeliramo li konzolu jednim elementom,
kao na prethodnoj slici,
dobit ćemo
![]() = 165, 731.
Upotrijebimo li tri elementa
(
= 165, 731.
Upotrijebimo li tri elementa
(
![]() = 1, 66667 m), bit će
= 1, 66667 m), bit će
![]() = 164, 510,
dok je za pet elemenata (
= 164, 510,
dok je za pet elemenata (
![]() = 1, 0 m)
= 1, 0 m)
![]() = 164, 496.
Očito je da pri `progušćenju' mreže niz konvergira
(odozgo) prema točnoj vrijednosti.
= 164, 496.
Očito je da pri `progušćenju' mreže niz konvergira
(odozgo) prema točnoj vrijednosti.
Kritična je sila
Pcrit = ![]() Pref ,
pa je, za model s pet elemenata,
Pcrit = 164, 496 . 1, 0 = 164, 496 kN.
Uzmemo li
Pref = 50, 0 kN ,
dobit ćemo
Pref ,
pa je, za model s pet elemenata,
Pcrit = 164, 496 . 1, 0 = 164, 496 kN.
Uzmemo li
Pref = 50, 0 kN ,
dobit ćemo
![]() = 3, 28992,
te je, ponovo,
Pcrit = 3, 28992 . 50, 0 = 164, 496 kN.
= 3, 28992,
te je, ponovo,
Pcrit = 3, 28992 . 50, 0 = 164, 496 kN.
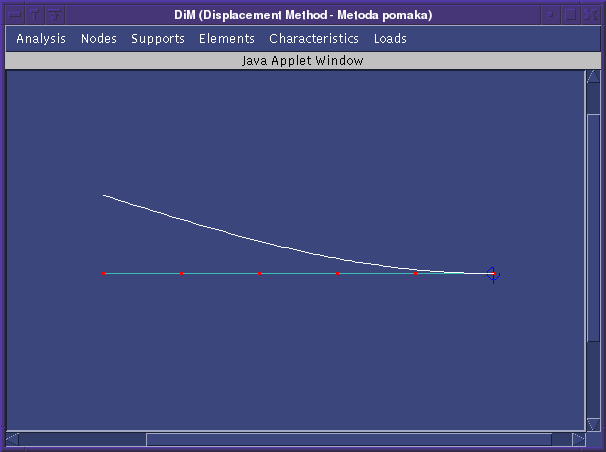
Na sljedećim su slikama prikazani, redom: približni izvijeni oblik konzole modelirane jednim elementom te model s pet elemenata i tako dobiveni približni izvijeni oblik. Približni se izvijeni oblik progušćenjem mreže sve više približava točnom obliku - četvrtini vala sinusoide.


Naglašavamo još jednom: sila Pref zadana je u čvoru 1, a ne kao sila na kraju elementa.
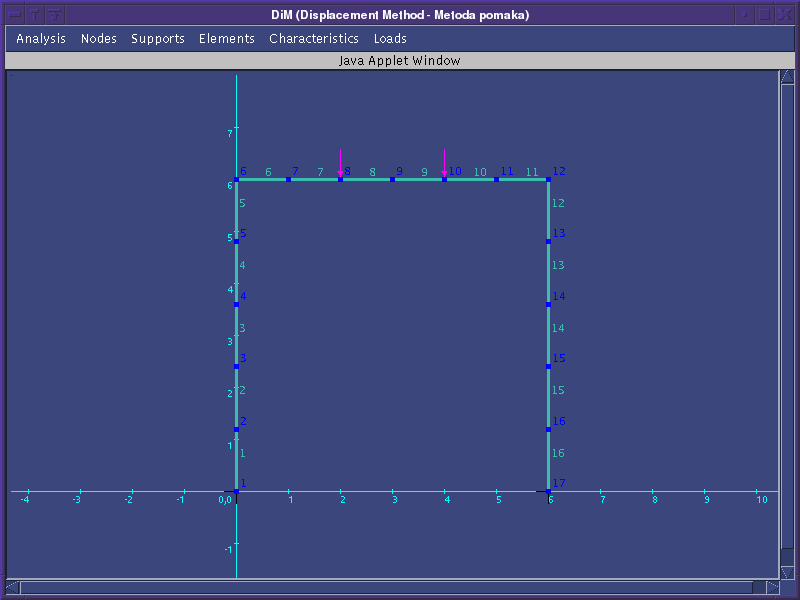
Nešto je složeniji primjer, također s poznatim analitičkim rješenjem, dvozglobni okvir prikazan na slici:
![\includegraphics[scale=1.25]{dim2.6}](img9.png)
Ako su h = ![]() i
EI = const, kritična je vrijednost
sila F:
i
EI = const, kritična je vrijednost
sila F:
Neka su:
![]() = 6, 0 m,
b/h = 10/20 [cm] i modul elastičnosti
E = 2 . 108 kN/m2; tada je
Fcrit = 657, 407 kN.
Zadamo li
Fref = 100, 0 kN ,
bit će
= 6, 0 m,
b/h = 10/20 [cm] i modul elastičnosti
E = 2 . 108 kN/m2; tada je
Fcrit = 657, 407 kN.
Zadamo li
Fref = 100, 0 kN ,
bit će
![]() = 6, 57407.
= 6, 57407.
Modeliramo li gredu i stupove s po jednim elementom,
kao na sljedećoj slici, dobit ćemo
![]() = 6, 75302.
= 6, 75302.

Na sljedećoj je slici prikazan približni oblik izvijene konstrukcije.
Modeliramo li stupove s po pet elemenata
(
![]() = 1, 2 m),
a gredu sa šest elemenata (
= 1, 2 m),
a gredu sa šest elemenata (
![]() = 1, 0 m),
bit će
= 1, 0 m),
bit će
![]() = 6, 73397.
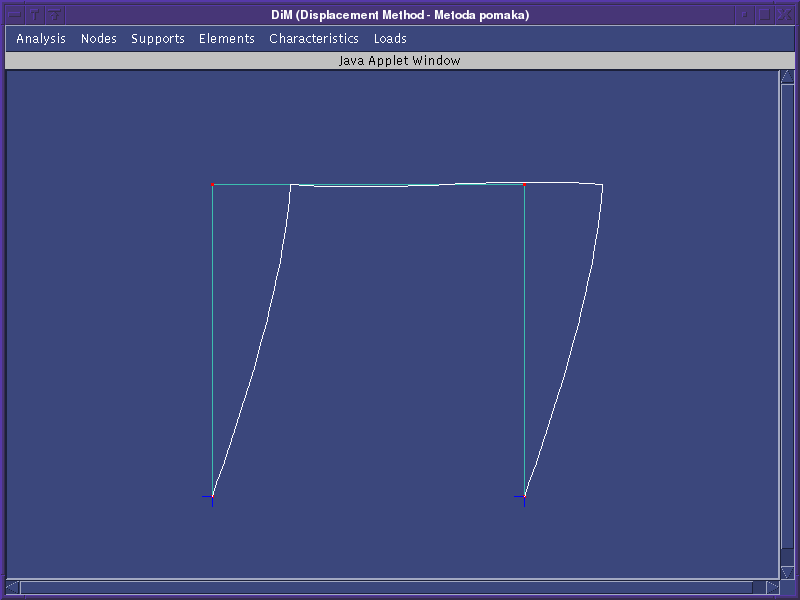
Model i približni izvijeni oblik prikazani su na sljedeće dvije
slike.
= 6, 73397.
Model i približni izvijeni oblik prikazani su na sljedeće dvije
slike.