 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
  |
Blaženka Divjak (bdivjak@foi.hr)
Notes on Taxicab GeometryThe taxicab geometry is one of non-Euclidean geometries. Hermann Minkowski (Gesammelte Abhandlungen) introduced this geometry more than 100 years ago. In this hundred years there were the periods of marginalization and the periods of great interest and wide application of this geometry. Today there is a whole specter of application and implementation of the taxicab geometry. There are several reasons for this.First, the taxicab geometry is similar to Euclidean geometry and easy to understand. It can be observed as such a metric system where the points correspond to the intersections of the streets in the imagined city, streets run only horizontally and \ vertically. There are no one-way streets. From the previous description the name taxicab geometry arises. The taxicab geometry is appropriate to discuss out during the undergraduate study in the form of essays, seminar works and diploma thesis as it is described in [7] and [9]. Second, the taxicab geometry is interesting for theoretical geometry study, too. It can be analyzed by synthetic approach (introduced by David Hilbert), or by metric approach ( described by George David Birkhoff). Mentioned approaches are described and discussed in [6]. There is the third approach in geometry using abstract groups and group theory. This approach was introduced by Felix Klein and Arthur Cayley. They claimed that geometry had to be studied through acting the group of motions on the given set. Further, some propositions about ellipses in the taxicab geometry are proved. Third, the practical value of the taxicab geometry is its wide application in (urban) transportation problems, city planning and so on. This application has been described in [10]. Keywords: non-Euclidean geometry, taxicab geometry  Article in PDF. Article in PDF.
|
 |
Radimir Viher (viher@grad.hr)
The Consequences of Descartes's Method for Factorization of 4th Degree PolynomialIn this article we give in details description of Descartes's method for factorization of the fourth degree polynomial (over the field R) in the following reduced form P4(x) = x4+a2x2+a1x+a0 = (x2+Ax+B)(x2+Cx+D). When we seek the solution for A we get the following cubic resolvent P3(t) = t3+2a2t2+(a22-4a0)t-a12, where t = A2. At the end, we formulate and prove two theorems. In the first one, we find the correspondences between the types of the roots of P3(t) and P4(x) while in the second one, we give the characterizations of types of roots for P3(t).Keywords: Descartes's method, factorization, cubic resolvent, types of roots, characterizations of types of roots, plane quartic curves  Article in PDF. Article in PDF.
|
  |
Zvonko Čerin (cerin@math.hr)
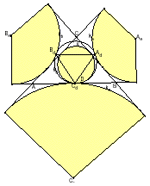
Triangles from the Feuerbach TriangleWe prove four unusual theorems about the Feuerbach triangle AdBdCd of the given triangle ABC whose vertices are points Ad, Bd, and Cd in which the excircles touch from outside the nine-point circle. These results concern the problem to determine for which triangles XYZ will the segments AdX, BdY, and CdZ be sides of a triangle. We shall find five triangles XYZ (including the degenerate triangle at the point D in which the incircle touches from inside the nine-point circle) associated to a triangle ABC such that AdX, BdY, and CdZ are never sides of a triangle. On the positive side, we discover three triangles XYZ such that the segments AdX, BdY, and CdZ are always sides of a triangle. We give an algebraic method of proof for these results based on simple analytic geometry in the plane. We also show how one can discover these and other related results using the Geometer's Sketchpad.Keywords: triangle, incircle, excircles, nine-point circle, Feuerbach triangle, central points, Feuerbach point, Geometer's Sketchpad ž  Article in PDF. Article in PDF.
|
  |
Miljenko Lapaine (mlapaine@public.srce.hr)
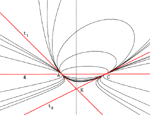
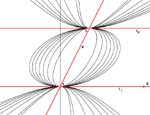
Conic Section Pencil Given by two Double PointsThe algorithm is presented for the determination of coefficients in the equation of conic section pencils when the pencil is given by four base points two of which are double points. In order to work with the points in infinity, the homogeneous coordinates are introduced. The approach is illustrated by several examples.Keywords: conic section pencil, homogeneous coordinates, computer graphics  Article in PDF. Article in PDF.
|
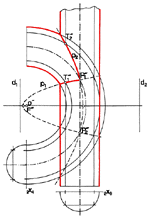 |
Ivanka Babić (ibabic@juraj.gradnz.grad.hr)
Torus and some of its Applications in Mechanical EngineeringSome characteristics of the open or ring torus such as the three systems of circle sections are pointed out in the article. The torus of this shape is applied in mechanical engineering for designing certain parts of machines. Some machine parts are obtained by the intersection of a surface of revolution and a plane, while some others are obtained by the intersection of surfaces of revolution. The example presented in the article shows how the body of a thrust bar and a pipe diverging which consist of a cylinder and a torus are created. The article emphasizes the simplicity of the construction of the projection of the intersection curves which derives from the geometric theory.Keywords: absolute conic, pipe diverging, ring torus, thrust bar  Article in PDF. Article in PDF.
|
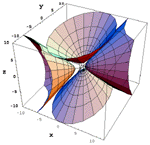 |
Jelena Beban-Brkić and Ivan Medved (beban@geodet.geof.hr)
The General Theory of Central Quadrics with MathematicaThis paper offers the procedure for recognising central quadrics graphs given by their equations in a general form as well as their classification. There has been a program made for the computer that computes eigenvalues and eigenvectors of the matrix of the associated quadratic form within the quadratic equation on the basis of ten initial general equation coefficients of the second order surface. It writes as well the canonical equation form of the surface, classifies and delineates the surface, if it is real, in the standard (canonical) as well as in the general position.Keywords: quadrics, linear operators, eigenvalues, eigenvectors, diagonalisation, quadratic form  Article in PDF. Article in PDF.
|
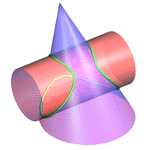 |
Željko Gjuranić (gjuro@grad.hr)
Drawing Intersection Curves by AutoCAD-aThis article presents the analitical derivation which was the base for designing the computer program for drawing the intersection curves of oblyque cones and cylinders with AutoCAD. The internet address where you can download this program and the instructions can be found in the article. There are some examples which are drawn by using this programme.Keywords: AutoCAD, intersection curves  Article in PDF. Article in PDF.
|
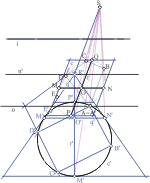 |
Ana Sliepčević (anasli@juraj.gradnz.grad.hr)
One Application of Perspective CollineatinThe aim of this paper is to remind us of some previous geometrical constructions derived by the means of a perspective collineation and an affinity. It should refresh the drawing in geometry. Nowdays it is much easier by using the computer. The tasks are solved with the method of the collinear corresponded figures. Each problem connected with a conic by using the method of a perspective collineation can be transformed into the elementary problem connected with a circle. It results with the geometricaly correct solution of the initial problem.Keywords: conic, perspective collineation, affinity  Article in PDF. Article in PDF.
|
 |
Sanja Filipan, Sonja Gorjanc and Hrvoje Kvasnička (sfilipan@grad.hr)
Roofing with a Parabolic ConoidThis articele presents the construction and equations for one type of 3th degree conoid. We defined with $Mathematica$ the functions for drawing and draw the pictures of the coniod, the graphics presentations of Gaussian and mean curvatures and the examples for roofing over the rectangular plan with a parabolic conoid.Ključne riječi: parabolic conoid, Mathematica  Article in PDF. Article in PDF.
|
Ruža Ostrogonac-Šešerko, Marifa S. Toralba, Erol Inelmen, Lidija Pletenac and Sing-E Lee
(rose@civil.uwa.edu.au)
Visual Communication Curricula for the Global EngineersThe first step in introducing the engineering profession to students is to develop good communication skills, especially graphics communication. In this paper authors from different parts of the world compare their current practices in delivering Engineering Graphics units (Descriptive Geometry, Manual Technical Drafting, Freehand Drawing Computer Graphics and CAD programs: AutoCAD.) in an attempt to map a path which the future curriculum in this area may follow. They propose what will stay as principles language and what is going to change.Keywords: engineering graphics, computer graphics, curriculum, future global engineers  Article in PDF. Article in PDF.
|