 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
| Gunter Weiss, Ana Sliepčević (Gunter.Weiss@tu-dresden.de)
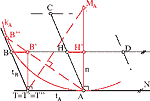
Osculating Circles of Conics in Cayley-Klein PlanesIn the Euclidean plane there are several well-known methods of constructing an osculating (Euclidean) circle to a conic. We show that at least one of these methods can be "translated" into a construction scheme of finding the osculating non-Euclidean circle to a given conic in a hyperbolic or elliptic plane. As an example we will deal with the Klein-model of these non-Euclidean planes, as the projective geometric point of view is common to the Euclidean as well as to the non-Euclidean cases.Key words: Cayley-Klein plane, elation, pencil of conics, osculating circle, curvature centre  Article in PDF. Article in PDF.
|
 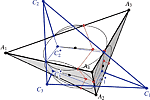 | Hans-Peter Schröcker (hans-peter.schroecker@uibk.ac.at)
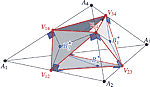
Orthologic Tetrahedra with Intersecting EdgesTwo tetrahedra are called orthologic if the lines through vertices of one and perpendicular to corresponding faces of the other are intersecting. This is equivalent to the orthogonality of non-corresponding edges. We prove that the additional assumption of intersecting non-corresponding edges ("orthosecting tetrahedra") implies that the six intersection points lie on a sphere. To a given tetrahedron there exists generally a one-parametric family of orthosecting tetrahedra. The orthographic projection of the locus of one vertex onto the corresponding face plane of the given tetrahedron is a curve which remains fixed under isogonal conjugation. This allows the construction of pairs of conjugate orthosecting tetrahedra to a given tetrahedron.Key words: orthologic tetrahedra, orthosecting tetrahedra, isogonal conjugate  Article in PDF. Article in PDF.
|
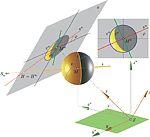  | Georg Glaeser, Karlheinz Schott (georg.glaeser@uni-ak.ac.at)
Geometric Considerations About Seemingly Wrong Tilt of Crescent MoonThe following phenomenon is well-known and again and again appears as an unanswered question in literature and on internet platforms: If you see moon and sun in the sky at the same time, then the (bisector of the) crescent moon in most cases does not seem to be precisely directed at the sun. Particularly at sunset, when you would expect the bisector of the crescent moon to be horizontal, it mostly points upwards. To "prove" that, photos that seem to support this view are displayed. In this paper it is shown by means of geometry what the "wrong moon tilt" is all about and that an explanation is to be found in the nature of central or normal projections (photography is basically a central projection, at an extremely long focal length it is approximately a normal projection). The paper also deals with the reason why the seemingly wrong tilt is subjectively felt. The path of the light from the sun to the moon is in any case displayed straight (apart from minor deviations due to refraction close to the horizon), except one takes photos with a fish-eye lens.Key words: Moon tilt, Terminator, Normal Projection  Article in PDF. Article in PDF.
|
 | Sonja Gorjanc (sgorjanc@grad.hr)
Pedal Surfaces of First Order CongruencesThis paper is an overview of the pedal surfaces Pnn+2 for first order line congruences. We describe their construction, prove their algebraic properties, derive parametric and implicit equations and visualize these new resulting surfaces with the program Mathematica in seven examples.Key words: congruence of lines, pedal surface of congruence, pinch-point, singular point  Article in PDF. Article in PDF.
|
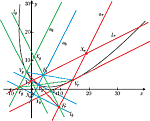 | Norman John Wildberger (n.wildberger@unsw.edu.au)
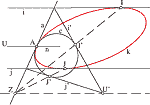
Chromogeometry and Relativistic ConicsThis paper shows how a recent reformulation of the basics of classical geometry and trigonometry reveals a three-fold symmetry between Euclidean and non-Euclidean (relativistic) planar geometries. We apply this chromogeometry to look at conics in a new light.Key words: chromogeometry, conics, relativistic geometry  Article in PDF. Article in PDF.
|
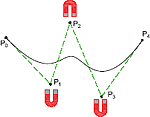 | Željko Gjuranić (Zeljko.Gjuranic@Emerson.com)
Conics and Graphs of Some Polynomials by Using NURBS CurvesThis paper presents the definition of conics and the graphs of the 3rd and 4th degree polynomials by using NURBS curves, with a special description of the beam deflection line. The usage in AutoCAD is presented.Key words: conics, NURBS curves, AutoCAD, beam deflection line  Article in PDF. Article in PDF.
|