Znanstveno-stručni časopis  
Hrvatskog društva za geometriju i grafiku  

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics

Vlasta Szirovicza (szvlasta@master.grad.hr) 

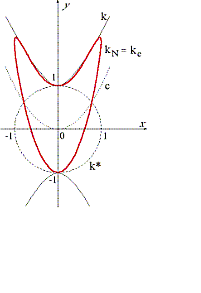
Pedal Curves of Conics in an Isotropic Plane

At first we introduce the notion of pedal curves in isotropic plane I2. Then we give a classification of curves of order 4, which are pedal of conics given by their normal forms with respect to the group G3 of isotropic similarities. Finally, we give a relationship between the pedals and the quadratic inversion for these curves in isotropic plane.

Article in PDF.
Ana Sliepčević (anasli@juraj.gradnz.grad.hr) 

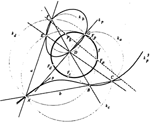
The Focal Curve of Fourfold Foci in the Pencil of 3th Order Circular Curves

In this paper it is proved that the curve of fourfold foci in the pencil of circular and rational cubics, which is deduced by ordinary inversion, is a circle, and its construction is shown. An analogus foci circle f is constructed in one pencil (ki3) of circular cubics of 1st genus. It is shown that by means of this circle focus of any cubics belonging to  (ki3) can be obtained.

Article in PDF.
Sonja Gorjanc (sgorjanc@master.grad.hr) 

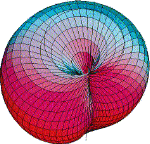
Pedal Surfaces of the (1,2) Congruence 

In this paper the pedal surfaces of the 1st order and 2nd class congruences are deduced by quartic inversion in projective space, using the methods of synthetic geometry. It is shown that there are the 4th order surfaces with a double line, and the constructive elaboration method is given. For one class of these surfaces the parametric equations are derived, and it is shown how they could be drawn using Mathematica. Some properties of the surfaces are proved and illustrated with the pictures drawn by Mathematica. 

Article in PDF.
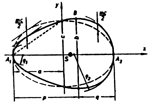György Nagy-Führer (fur@efe.hu) 

Drawing of Bird-egg Forms

Using Maple V we compared the data of original bird-eggs given by Jacab with the theoretical results given by Wunderlich. It turned out that for the eggs of the bird Sterna hirundo the parabolic cubic and the Kirste profile seem to be almost identical, and their plots coincide with the curves drawn by oologists. But, for the eggs of the birds Sterna paradisaea and Sterna dougallii differences are greater.

Article in PDF.
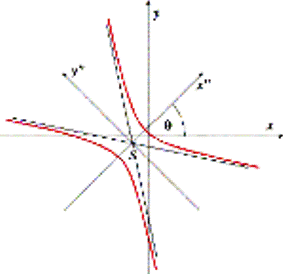Miljenko Lapaine i Damjan Jovičić (miljenko.lapaine@public.srce.hr) 

Computer-aded Graphical Representation of Conic Sections

The paper presents a detailed  classification of conic sections or second order curves. The conic sections are first classified into central and non-central, and then to their subtypes. The purpose of such classification is to obtain analytical apparatus by means of which the necessary conclusions about the conics can be made and furthermore, graphically presented on the basis of given coefficients being included into the general form of the conic section equation. In order to draw arbitrary curves, and also conic sections by means of computer, it is very convenient to use their equations in parametric form. Therefore, the corresponding equation in the parametric form have been suggested for each type of the conic section. A numeric example has been given for each type of the conic section.

Article in PDF.
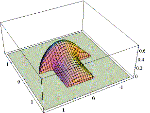Josip Dvornik (dvornik@master.grad.hr) 

Generating Smooth Functions on Compound Domain by R-functions

The analytical procedure for generating smooth functions on compound domain is described. This procedure is based on the R-function method developed by Ukranian mathematician L. V. Rvačev. The R-functions are ordinary continous functions of continous variables, but the analogy with Bool functions in mathematical logics makes their generating easier. In this paper the computer program for generating and drawing R-functions in central projection is presented. The program has been made in Mathematica language. The application of program has been illustrated through several examples.

Article in PDF.
Lidija Pletenac (pletenac@master.gradri.hr) 

New Aspect of Education in Descriptive Geometry

Descriptive Geometry still has its old importance for technical sciences, and new aims too. This subject prepares students for CAD, which is necessary in technical education, but after Descriptive Geometry and Introduction to computer sciences. I present some new aspects of education in Descriptive Geometry, use of CAD during lectures and new exercises with interactive computer graphics, especially in Applied Geometry.

Article in PDF.