Znanstveno-stručni časopis
Hrvatskog društva za geometriju i grafiku

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics

Boris Odehnal (boris.odehnal@uni-ak.ac.at)

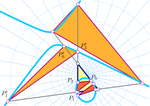
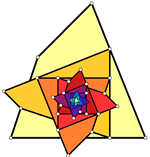
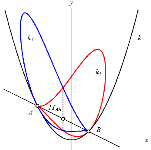
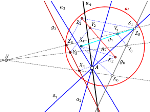
Dva konvergentna niza trokuta

Poluortogonalan put je poligonalna linija upisana u dani mnogokut takva da je i-ta stranica poligonalne linije okomita na i-tu stranicu danog mnogokuta. U slučaju trokuta, zatvoreni poluortogonalni putovi su trokuti slični danom trokutu. Iteracijom konstrukcije poluortogonalnih putova u trokutima dobivaju se beskonačni nizovi upisanih sličnih trokuta. Pokazujemo da ova dva različita niza konvergiraju prema bicentričnom paru Brocardovih točaka trokuta. Nadalje, veza s diskretnim logaritamskim spiralama omogućuje vrlo jednostavnu, elementarnu i novu konstrukciju limesa ovih nizova, Brocardovih točaka. Iznosimo i neke napomene o poluortogonalnim putovima kako u neeuklidskim geometrijama i tako i za n-kute.

Ključne riječi: trokut, poluortogonalan put, Brocardove točke, sjecište simedijana, diskretna logaritamska spirala, Tucker-Brocardova kubika

Article in PDF.

 


Zdenka Kolar-Begović, Ružica Kolar-Šuper, Vladimir Volenec (zkolar@mathos.hr, rkolar@foozos.hr, volenec@math.hr )

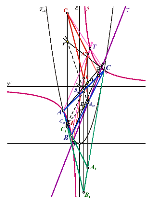
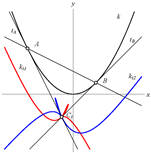
Jeřabekova hiperbola trokuta u izotropnoj ravnini

U radu proučavamo Jeřabekovu hiperbolu dopustivog trokuta u izotropnoj ravnini. Istražujemo različite načine generiranja ove specijalne hiperbole i izvodimo njenu jednadžbu u slučaju standardnog trokuta. Dokazujemo da neke značajne točke trokuta u izotropnoj ravnini leže na toj hiperboli čiji je centar u Feuerbachovoj točki trokuta. Proučavamo i neka druga zanimljiva svojstva ove hiperbole i njezinu vezu s nekim značajnim elementima trokuta u izotropnoj ravnini.

Ključne riječi: dopustivi trokut, standardni trokut, Jeřabekova hiperbola

Article in PDF.

Ema Jurkin (ema.jurkin@rgn.hr)

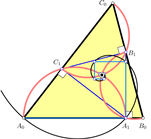
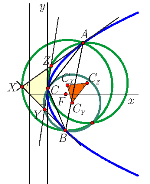
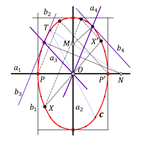
Krivulje Brocardovih točaka u pramenovima trokuta u izotropnoj ravnini

U radu se promatra pramen trokuta sa zajedničkom opisanom kružnicom. Pokazuje se da Brocardove točke tih trokuta leže na dvije krivulje 4. reda.

Ključne riječi: izotropna ravnina, pramen trokuta, Brocardove točke


Article in PDF.

Si Chun Choi, N.J. Wildberger (si.choi@det.nsw.edu.au, n.wildberger@unsw.edu.au)

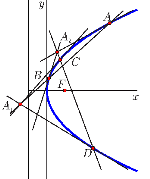
Univerzalna parabola

Dokazujemo neka klasična svojstva kao i neke nove činjenice o paraboli koristeći okvir racionalne trigonometrije. Proširujemo proučavanje konika na opća polja.


Ključne riječi: parabola, racionalna trigonometrija, konika

Article in PDF.


Gunter Weiss (weissgunter@gmx.at)

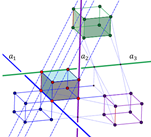
Nov pogled na teorem tri simetrije

U euklidskoj ravnini poznato je da je produkt tri simetrije ponovo simetrija ako i samo ako se njihove osi sijeku u jednoj zajedničkoj točki. Takožđer poznat je i neeuklidski analogon "teorema tri simetrije" (3RT), vidi npr. [4]. U ovom članku predstavljene su afine verzije tog teorema tako da se proučavaju tri mimosmjerne simetrije kojima se osi sijeku u jednoj točki. Pokazat će se da je važno, u svim verzijama 3RT-a, da se tri para (os, smjer simetrije) danih (mimosmjernih) simetrija mogu proučavati kao involutivni projektivitet. Za euklidski i neeuklidski slučaj ovo svojstvo je automatski ispunjeno. Sa stajališta projektivne geometrije (mimosmjerna) simetrija je harmonička homologija. U afinoj geometriji simetrija je indirektna involutivna transformacija, dok u projektivnoj geometriji nema smisla govoriti o "direktnoj" i "indirektnoj" transformaciji. Harmonička homologija dopušta interpretaciju i kao osnu simetriju i kao centralnu simetriju. Ipak, može se proučavati produkt triju harmoničkih homologija koji je ponovno harmonička homologija. Nekim posebnim mežđusobnim položajima centara i osi danih homologija može se dobiti elacija ili čak identitet. Posljedica danih rezultata su daljnje generalizacije 3RT-a, npr. u ravninama s Minkowski metrikom, a nim ili projektivnim 3-dimenzionalnim prostorima ili u geometrijama kružnice.


Ključne riječi: teorem tri simetrije, osna simetrija, harmonička homologija, involutivni projektivitet

Article in PDF.