 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
| Zdenka Kolar-Begović (zkolar@mathos.hr)
Afino pravilan ikozaedar upisan u afino pravilan oktaedar u GS-kvazigrupiKvazigrupa zlatnog reza ili kraće GS-kvazigrupa idempotentna je kvazigrupa u kojoj vrijede identiteti
a(ab\(\cdot\)c)\(\cdot\)c=a\(\cdot\)(a\(\cdot\)bc)c=b. Pojam GS-kvazigrupe uveo je
VOLENEC. Razni geometrijski pojmovi mogu biti uvedeni
u GS-kvazigrupi pomoću binarne operacije te kvazigrupe.
Korištenjem relacija i identiteta u općoj GS-kvazigrupi u
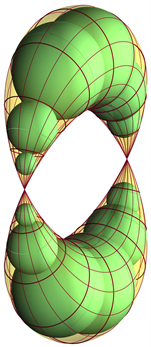
ovom je radu pokazano da se svakom afino pravilnom oktaedru može upisati afino pravilan ikozaedar. Geometrijski
prikaz u kvazigrupi \(\mathbb{C}(\frac{1}{
2} (1+\sqrt{5}))\) pokazuje kako geometrijske tvrdnje mogu biti posljedica potpuno algebarskih
razmatranja. |
| Harun Bariş Çolakoğlu (hbcolakoglu@akdeniz.edu.tr)
Trigonometrijske funkcije u m-ravniniU članku definiramo trigonometrijske funkcije u ravnini s m-metrikom. Zatim pokazujemo dva svojstva ovih trigonometrijskih funkcija gdje jedno od njih daje formulu površine trokuta u m-ravnini s primjenomm-metrike. Ključne riječi: Taxicab metrika, metrika kineskog šaha, alfa metrika, m-metrika, m-trigonometrija  Article in PDF. Article in PDF. |
|
| Ema Jurkin, Marija Šimić Horvath, Vladimir Volenec (ema.jurkin@rgn.hr, marija.simic@arhitekt.hr, volenec@math.hr)
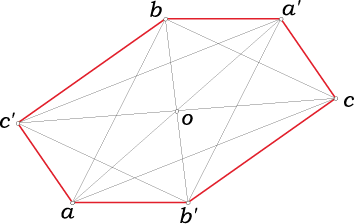
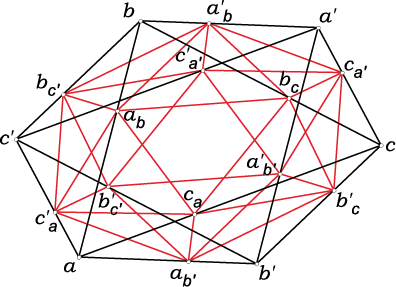
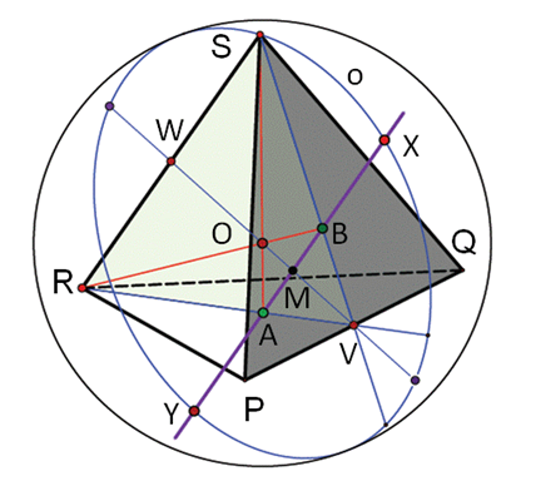
O Brocardovim točkama harmoničkog četverokuta u izotropnoj ravniniU radu se prikazuju neki novi rezultati o Brocardovim
točkama harmoničnog četverokuta u izotropnoj ravnini.
Konstruiraju se novi harmonični četverokuti pridruženi
danom četverokutu, te se proučavaju njihova svojstva
vezana uz Brocardove točke. |
|
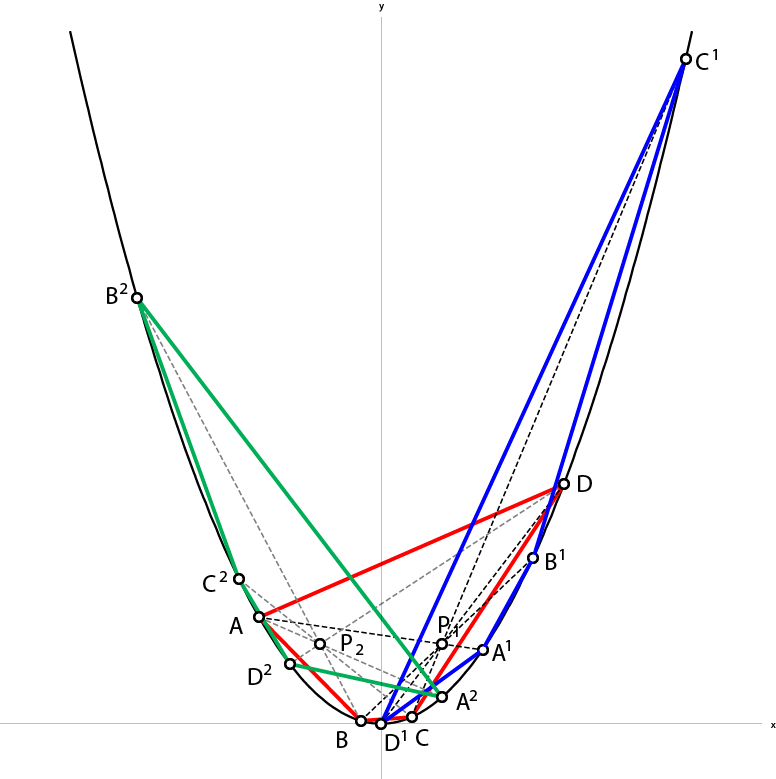
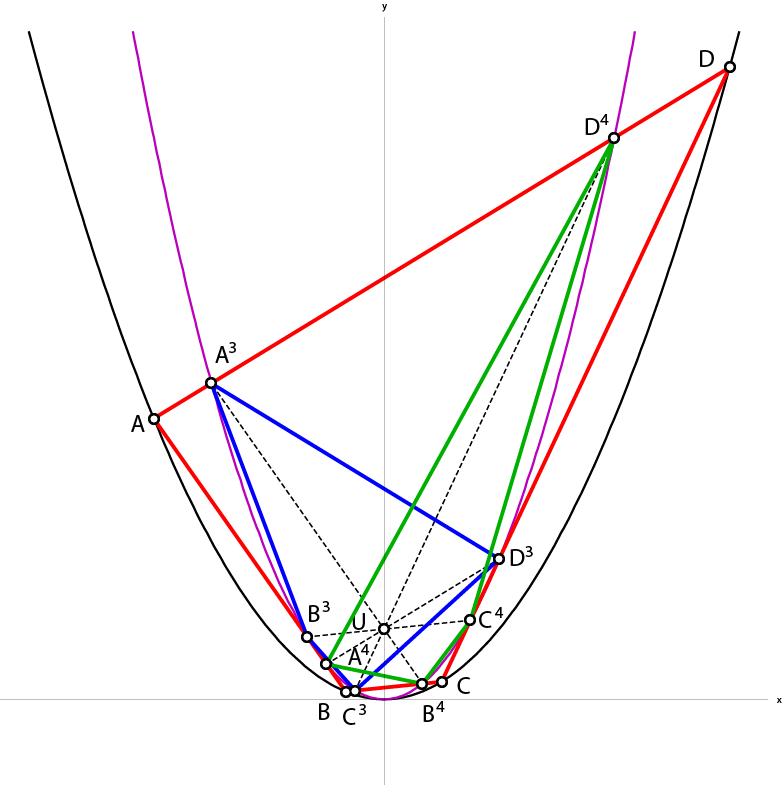
| Iva Kodrnja, Helena Koncul (ikodrnja@grad.hr, hkoncul@grad.hr)
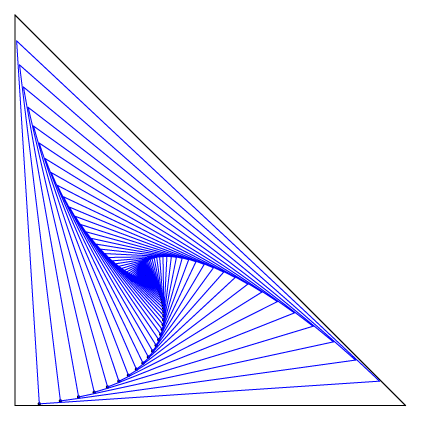
Geometrijsko mjesto vrhova nedijalnog trokutaU ovom članku proučavaju se nedijane i nedijalni trokuti omjera \(\eta\) za dani trokut. Određuju se geometrijska mjesta vrhova nedijalnih trokuta za \(\eta\in \mathbb{R}\) te ih se povezuje s pojmom izotomično konjugiranih točaka danog trokuta. Nadalje, određuje se krivulja na kojoj leže vrhovi nedijalnih trokuta za čvrsti \(\eta\) kada se iteriraju nedijalni trokuti. |
|
| Gunter Weiss (weissgunter@hotmail.com)
Nestandardni pristupi nizovima Fibonaccijevog tipaFibonaccijev niz i zlatni rez, limes kvocijenata susjednih Fibonaccijevih brojeva, su pojmovi poznati ne samo matematičarima i geometričarima, već gotovo svima. Oni svoju primjenu nalaze u umjetnosti i arhitekturi. Poznato je nekoliko pokušaja poopćenja ovih pojmova, kao što su nizovi brojeva i kvadratne jednadžbe koje rezultiraju takozvanim "metalnim rezovima" V. DE SPINADEL [8], ili kubni "plastični broj" VAN DER LAANA [5], odnosno "kubni omjer" L. ROSENBUSCHA [7]. Spomenuta se poopćenja odnose na nizove cijelih ili realnih brojeva. "Nestandardnim pristupima" ovdje smatramo poopćenja u odnosu na dano polje ili prsten brojeva, kao i na vizualizaciju dobivenih geometrijskih objekata. Idući se pristup odnosi na Fibonaccijev, odnosno Padovanov tip kombinacija danih početnih objekata. Pokazuje se da pojam zlatnog reza ili van der Laanovog reza ima smisla promatrati i za vektore, matrice i preslikavanja.
|
|
| Boris Odenhal (boris.odehnal@uni-ak.ac.at)
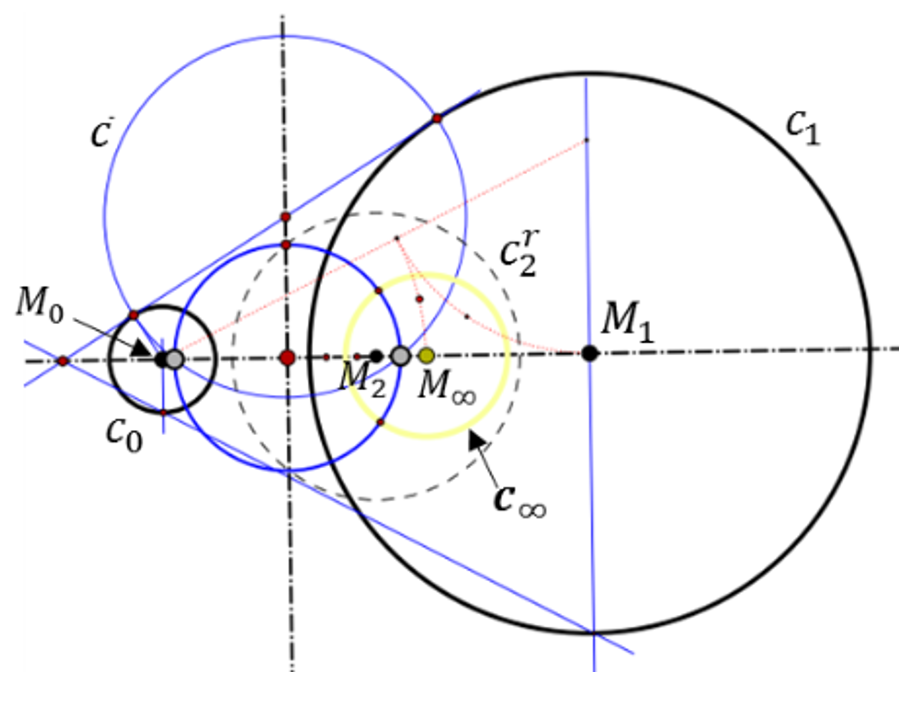
Poopćene konhoidePrilagođavamo klasičnu definiciju konhoida iz euklidske ravnine geometrijama definiranim kvadrikama. Postiže se poopćena konhoidna transformacija koja se temelji na konstrukciji pomoću dvoomjera. Proučavaju se osnovna svojstva ovakve transformacije. Djelovanje poopćene konhoidne transformacije se proučava na nekim istaknutim primjerima kao što su pravčasta i sferna geometrija. Prikazuju se linearne i nelinearne transformacije te su opisane veze s dobro poznatim transformacijama.
|
|
| Norman J. Wildberger (n.wildberger@unsw.edu.au)
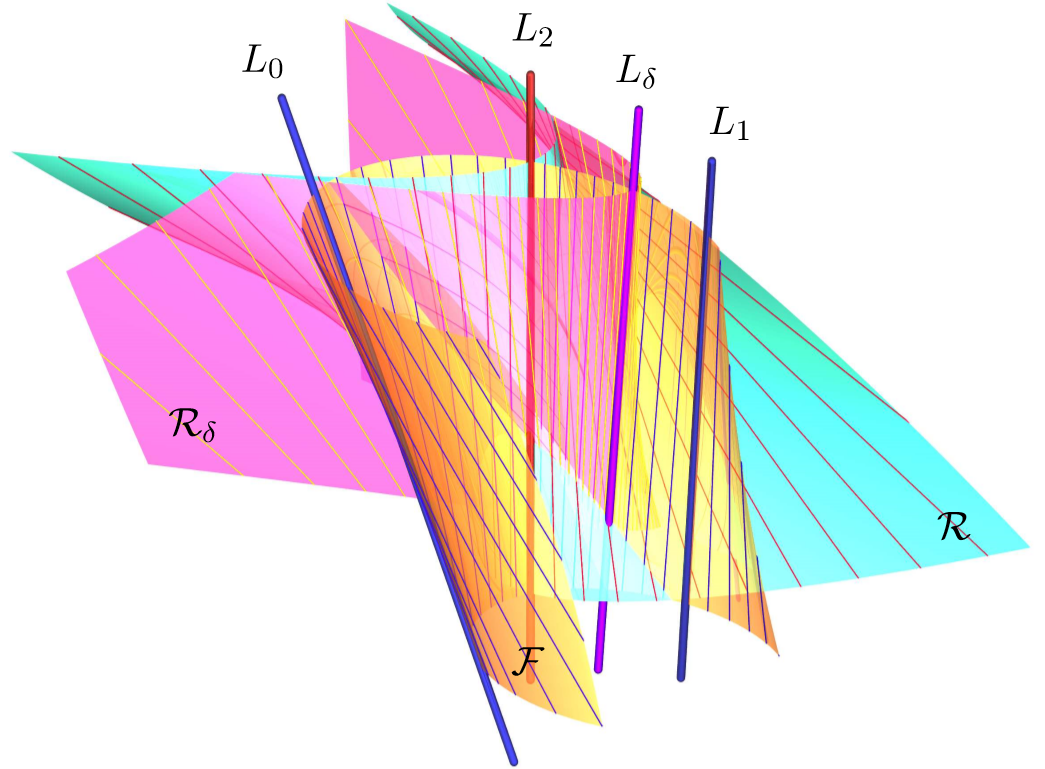
Racionalna trigonometrija u višim dimenzijama i dijagonalno pravilo za 2-ravnine u 4-dimenzionalnom prostoruProšrujemo racionalnu trigonometriju na više dimenzije tako da uvodimo racionalne invarijante između k-podprostora n-dimenzionalnog prostora. Dajemo alternativu kanonskim ili glavnim kutovima, koje su proučavali Jordan i mnogi drugi, te njihove varijante. Posebno proučavamo križni produkt, raspon i det-križni produkt 2- podprostora 4-dimenzionalnog prostora i pokazujemo da Pitagorin teorem, ili dijagonalno pravilo, ima prirodnu generalizaciju za takve 2-podprostore.
|
|
| Bojan Janjanin, Jelena Beban-Brkić (janjanin.bojan@gmail.com,
jbeban@geof.hr)
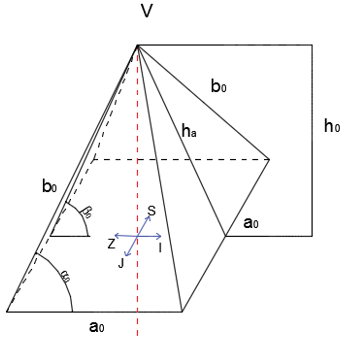
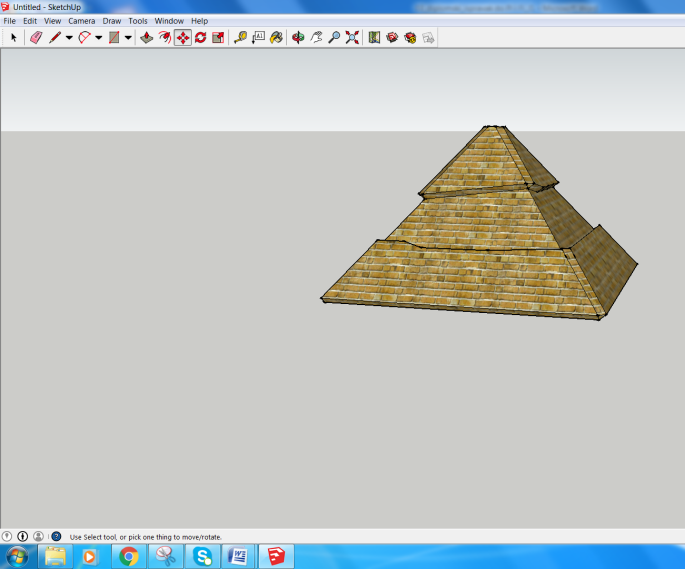
Analiza izmjere Keopsove piramideTema ovog rada jest analiza izmjere Keopsove piramide, najznačajnije od triju većih piramida Giza kompleksa, arheološkog nalazišta na visoravni Giza, na periferiji Kaira. Pretpostavlja se da je Keopsova, kao i Kefrenova i Mikerinova piramida građena u periodu 2686. - 2181. pr. Kr., u povijesti poznatom kao Staro egipatsko Kraljevstvo. Cilj nam je bio prikupiti podatke o geodetskoj izmjeri Keopsove piramide te ih analizirati. Uz to je opisano i što je prethodilo izgradnji takve monumentalne građevine. Navedeno je nekoliko hipoteza koje su vezane za način gradnje piramide te su opisane i moguće svrhe same gradnje. Pri analizi izmjere neprestano se pojavljuju dva broja koja su nazivana i "dva blaga geometrije", a to su broj Pi (\(\pi\)) zlatni rez odnosno zlatni broj Fi (\(\varphi\)). Upravo tim brojevima posvećeno je jedno poglavlje ovog rada.
|