Znanstveno-stručni časopis
Hrvatskog društva za geometriju i grafiku

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics

 



Márta Szilvási-Nagy, Szilvia Béla (szilvasi@math.bme.hu, belus@math.bme.hu)

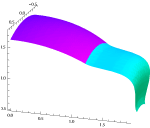
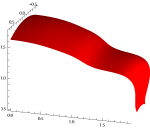
Simboličko spajanje B-splajn krivulja

Predstavljamo algoritam za spajanje B-splajn krivulja, koji se razlikuje od općenito upotrebljavane metode najmanjih kvadrata. Naš cilj je naći simboličko rješenje za ujedinjavanje kontrolnih poligona lukova koji se svaki zasebno opisuju kao B-splajn krivulje 4. stupnja. Također pokazujemo utjecaj uvjeta interpolacije i postizanja glatkih funkcija.

Ključne riječi: B-splajn krivulja, B-splajn ploha, integriranje, interpolacija, postizanje glatkoće

Članak u PDF-u.



Hiroshi Okumura (hiroshiokmr@gmail.com)

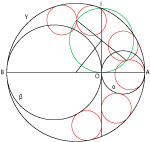
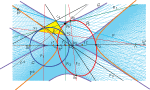
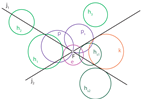
Lamoenove kružnice kolinearnog arbelosa

Pokazujemo beskonačne skupove kružnica koje generiraju
Arhimedove kružnice kolinearnog arbelosa.

Ključne riječi: arbelos, kolinearni arbelos, potencijalna
kružnica, Lamoenova kružnica

Članak u PDF-u.

 




Norman John Wildberger, Ali Alkhaldi (n.wildberger@unsw.edu.au, aalkaldy@hotmail.com)

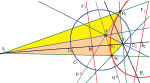
Parabola u univerzalnoj hiperboličkoj geometriji I

Uvodimo novu definiciju parabole u okvir univerzalne hiperboličke geometrije, pokazujemo mnoge analogone s
euklidskom geometrijom, ali i neka izvanredna nova svojstva. Osnovna je tehnika uspostavljanje paraboličnih standardnih koordinata u kojima parabola ima jednadžbu oblika xz = y2. Ističemo otkriće parabole blizanke, vezu sa sidtočkama, mnoge neočekivane konkurentnosti i kolinearnosti, konstrukciju evolute te odredivanje (do najviše) četiriju točaka parabole u kojima normale parabole prolaze jednom točkom.

Ključne riječi: univerzalna hiperbolička geometrija, parabola

Članak u PDF-u.

 


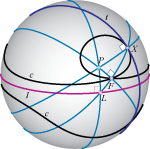
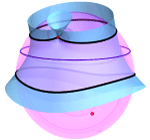
Boris Odehnal (boris.odehnal@uni-ak.ac.at)

Konhoide na sferi

Konstrukcija ravninskih konhoida može se prenijeti na euklidsku jediničnu sferu. Promatramo slučaj konhoida generiranih sfernim pravacima i kružnicama. Neke elementarne konstrukcije tangenata i kružnica zakrivljenosti vrijede i za sferne konhoide. Nadalje, naš je cilj ilustracija i precizan opis algebarskih svojstava glavnih pogleda sfernih konhoida, tj. slika konhoida pri ortogonalnom projiciranju na njihove ravnine simetrije.

Ključne riječi: krivulje na sferi, konhoide, algebarske krivulje, tangenta, kružnica zakrivljenosti, singulariteti, ortogonalna projekcija

Članak u PDF-u.

 

 


Géza Csima, Jenö Szirmai (csgeza@math.bme.hu, szirmai@math.bme.hu)

O izooptičkim hiperplohama u
n-dimenzionalnom euklidskom prostoru

Teorija o izooptičkim krivuljama dosta se proučava u euklidskoj ravnini E2 (vidi [1] i [13] te u referencama koje se tamo mogu naći). Autori su proučavali analogno pitanje u hiperboličkoj H2 i eliptičkoj ravnini E2 (vidi [3], [4]), međutim u višedimenzionalnim prostorima nema rezultata vezanih za ovu temu.
U ovom članku dajemo prirodno proširenje pojma izooptičkih krivulja na n-dimenzionalni euklidski prostor En (n≥ 3) koje zovemo izooptičke hiperplohe. Razvijamo algoritam kojim odredujemo izooptičke hiperplohe HD proizvoljne (n − 1)-dimenzionalne kompaktne parametarske domene D koja leži u hiperravnini u n- dimenzionalnom euklidskom prostoru.
Odredit ćemo jednadžbu izooptičkih hiperploha pravokutnika
D  E2 i vizualizirati ih koristeći program Wolfram Mathematica. Štoviše, pokazat ćemo neke moguće primjene izoptičkih hiperploha.

Ključne riječi: izooptičke krivulje, hiperplohe, diferencijalna geometrija, eliptička geometrija
Članak u PDF-u.

 

 


Ana Sliepčević, Ivana Božić, Helena Halas (anas@grad.hr, ivana.bozic@tvz.hr, hhalas@grad.hr)

Uvod u planimetriju kvazi-hiperboličke ravnine

Kvazihiperbolička ravnina je jedna od devet projektivno metričkih ravnina kojoj je apsolutna figura uređena trojka
{ j1, j2,F}, gdje su j1 i j2 realni pravci koji se sijeku u realnoj točki F. U ovom članku uvodimo neke osnovne pojmove za kvazihiperboličku ravninu, te dajemo klasifikaciju konika u odnosu na njihov položaj prema apsolutnoj figuri. Nadalje, uvesti ćemo pojmove vezane uz konike u kvazihiperboličkoj ravnini i pokazati nekoliko izabranih konstrukcija vezanih uz konike.

Ključne riječi: kvazihiperbolička ravnina, okomite točke,
centrala, klasifikacija qh-konika, oskulacijske qh-kružnice

Članak u PDF-u.


Maria Čuljak (culjakmaria1@gmail.com)

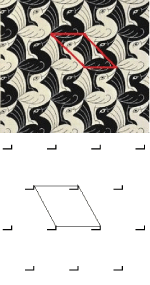
Izometrije u Escherovim radovima

U ovom članku dan je pregled izometrija ravnine i klasifikacija ravninskih grupa simetrija kao matematička podloga za razumijevanje "trikova" kojima se M. C. Escher služio prilikom stvaranja velikog broja svojih grafika. Razmatrat ćemo grupe simetrija na primjerima nekih od najpoznatijih Escherovih grafika.

Ključne riječi: Escher, izometrije, popločavanje, ravninske grupe simetrija

Članak u PDF-u.