 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
| Márta Szilvási-Nagy, Szilvia Béla (szilvasi@math.bme.hu, belus@math.bme.hu)
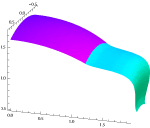
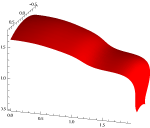
Stitching B-spline Curves SymbolicallyWe present an algorithm for stitching B-spline curves,
which is different from the generally used least square
method. Our aim is to find a symbolic solution for unifying
the control polygons of arcs separately described as 4th degree B-spline curves. We show the effect of interpolation
conditions and fairing functions as well.  Article in PDF. Article in PDF. |
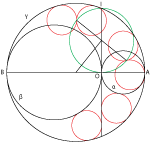
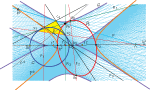
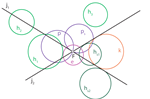
| Hiroshi Okumura (hiroshiokmr@gmail.com)
Lamoenian Circles of the Collinear ArbelosWe give an infinite sets of circles which generate
Archimedean circles of a collinear arbelos. |
|
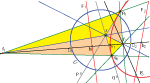
| Norman John Wildberger, Ali Alkhaldi (n.wildberger@unsw.edu.au, aalkaldy@hotmail.com)
The Parabola in Universal Hyperbolic Geometry IWe introduce a novel definition of a parabola into the
framework of universal hyperbolic geometry, show many
analogs with the Euclidean theory, and also some remarkable new features. The main technique is to establish
parabolic standard coordinates in which the parabola has
the form xz = y2. Highlights include the discovery of the
twin parabola and the connection with sydpoints, many
unexpected concurrences and collinearities, a construction
for the evolute, and the determination of (up to) four
|
|
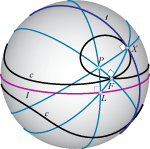
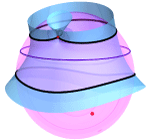
| Boris Odehnal (boris.odehnal@uni-ak.ac.at)
Conchoids on the SphereThe construction of planar conchoids can be carried over
to the Euclidean unit sphere. We study the case of conchoids of (spherical) lines and circles. Some elementary
constructions of tangents and osculating circles are stil
valid on the sphere. Further, we aim at the illustration
and a precise description of the algebraic properties of the
principal views of spherical conchoids, i.e., the conchoid's
images under orthogonal projections onto their symmetry
planes. |
|
| Géza Csima, Jenö Szirmai (csgeza@math.bme.hu, szirmai@math.bme.hu)
On the Isoptic Hypersurfaces in the
|
|
| Ana Sliepčević, Ivana Božić, Helena Halas (anas@grad.hr, ivana.bozic@tvz.hr, hhalas@grad.hr)
Introduction to the Planimetry of the Quasi-
|
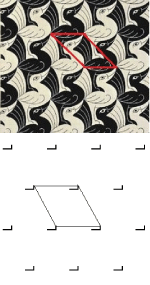
| Maria Čuljak (culjakmaria1@gmail.com)
Isometries in Escher's WorkFor better understanding of M. C. Escher's tesselation graphics we provide an overview of planar isometries and classification of plane symmetry groups. Some of the plane symmetry groups are explained on prominent Escher's graphics.Key words: Escher, isometries, tessellation, plane sym- metry groups  Article in PDF. Article in PDF. |