 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
  |
Hellmuth Stachel (stachel@geometrie.tuwien.ac.at)
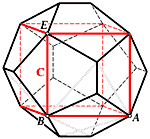
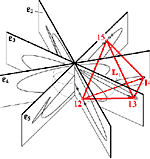
On the Tetrahedra in the DodecahedronThe 60 edges of the ten tetrahedra inscribed in a regular pentagon-dodecahedron form the so-called Gr"unbaum framework. It is already known that this structure is flexible. There are one-parameter motions which preserve the symmetry with respect either to a face axis or to a vertex axis. The paper treats analytical representations of these motions. Furthermore it is proved that both motions can blend into two-parametric motions which do not preserve any symmetry. Article in PDF. Article in PDF. | |
|
|
||
 |
Vlasta Szirovicza, Ana Sliepčević (szvlasta@juraj.gradnz.grad.hr)
The Analog of the Czuber's theorem in the isotropic planeThe paper proves that in the isotropic plane Czuber's theorem is valid only for the cubics of the second degree of circularity and for the completely circular cubics of the type tridens.Key words: geometry, isotropic plane, circular cubic, Czuber's theorem  Article in PDF. Article in PDF. | |
|
|
||
  |
Daniela Velichová (velichov@sjf.stuba.sk)
Density of Interior Points Distribution in Modelling of HyperpatchesThe paper deals with the modelling of hyperpatches (solid cells) on the basis of their creative representations and with the calculations of some intrinsic geometric properties of hyperpatches. The analytic representation of the hyperpatch in the form of a vector function of three variables provides the possibility to calculate and to control geometric properties and the density of distribution (homogeneous or non-homogeneous) of the hyperpatch interior points.Key words: hyperpatch modelling, geometric properties, density of interior points  Article in PDF. Article in PDF. | |
|
|
||
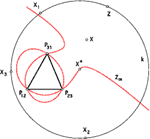 |
Gert Meinl (meinl@math.tu-dresden.de)
Closure Theorems at Triangles in the Sphere of WALLACE-SIMSON TheoremThe WALLACE-SIMSON theorem is considered ([4]) as one of the most beautiful theorems in the field of Geometry of triangles. Especially its importance for plane kinematics ([2,5]) is the starting point for discussing some classical but also new theorems in the sphere of the WALLACE-SIMSON theorem so far not found in any literature. The paper deals with some characteristic points and curves, if we reflect a point at the sides of a triangle.Key words: Wallace--Simson theorem, homological positions, polar triangle  Article in PDF. Article in PDF. | |
|
|
||
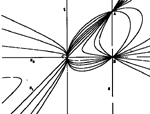 |
Miljenko Lapaine (mlapaine@public.srce.hr)
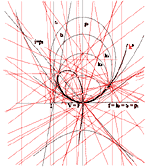
Conic Section Pencil Given by a Double Point and Two Single Real PointsThe algorithm is presented for the determination of coefficients in the equation of the type IV conic section pencils when the pencil is given by three base points one of which is a double point. In order to work with the points in infinity, the homogeneous coordinates are introduced. The approach is illustrated by several examples.Key words: conic section pencil, homogeneous coordinates, computer graphics  Article in PDF. Article in PDF. | |
|
|
||
 |
Dagmar Szarková (szarkova@sjf.stuba.sk)
A New Approach to the Computer Aided Calculation of Points on the Envelope Helical Surface CharacteristicsPresented calculations and the choice of variables u,vÎ[0,1] as curvilinear on the given basic surface φ enable the creation of a versatile programme for the graphical processing of the characteristics not only of the envelope helical, but also rotational surface F defined by the basic rotational surface φ. Basic surface φ can be generated from the basic curve c determined by (1) applying a class of revolutions about the coordinate axis x defined by the matrixTR(v), for vÎ[0,1] (2), that is positioned in the space by the transformation T (3). The envelope helical surface F can be created by helical movement of the points on the characteristics. The axis o of the helical movement located into the coordinate axis z is the axis of the surface F. Key words: envelope surface, envelope helical surface, envelope rotational  Article in PDF. Article in PDF. | |
|
|
||
 |
Vinko Mandekić-Botteri (vinko@zagreb.tekstil.hr)
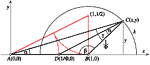
On the Constructions of the Golden TrianglesThis article proves that there exist the infinite number of the golden triangles ABC, with sides AB=1 andBC=(51/2-1)/2. It is derived the inequality which must satisfy the angle at a vertex A of each of these triangles, and it is shown that two isosceles and two right golden triangles are between them. Key words: golden section, golden triangle  Article in PDF. Article in PDF. | |